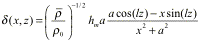,                            (1)

where 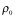 is the basic state density, h_m is the mountain height, a is the mountain half width, and l is the Scorer parameter, which is defined as the following for an isothermal atmosphere (Durran and Klemp 1982)

,                                         

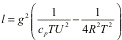where T is the temperature, R is the dry constant, and C_p the specific heat at constant pressure.  The mountain profile, h(x), is a witch of Agnesi curve,

.

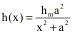The vertical velocity can be obtained from

w=Ud_x.                                                           (2)

            The analytic solution for the vertical velocity computed from (1) and (2) for an atmosphere with T=250K, U=20 m s^-1, a=10 km and h_m=1 m is shown in Fig. 1a.  As an example from two numerical models, the steady state vertical velocity obtained from the atmospheric portion of the Coupled Ocean-Atmosphere Mesoscale Prediction System (COAMPS; Hodur 1997) and the WRF-ARW is shown in Figs. 1b and 1c for Ut/a=30 or t=15,000 s.  At the COAMPS model top, a radiation boundary condition is used to mitigate the reflection of waves following Klemp and Durran (1983) and Bougeault (1983) while in WRF-ARW a Rayleigh damping sponge layer is used.  In this application, the finite difference schemes are of second-order accuracy in time and space for COAMPS and third-order in time and fifth-order in space for WRF.  The domains consists of 41x121 points (80x30 km) with grid intervals of Dx=2 km and Dz=250 m.  In both models, the compressible equations are integrated efficiently using a time splitting technique through the use of a semi-implicit formulation for the vertical acoustic modes (Klemp and Wilhelmson, 1978; Skamarock and Klemp 1994).  The small mountain height of 1 m, assures that the nonlinear contributions can be ignored.  The nonhydrostatic contribution is minimal as well because Na/U>>1.

 

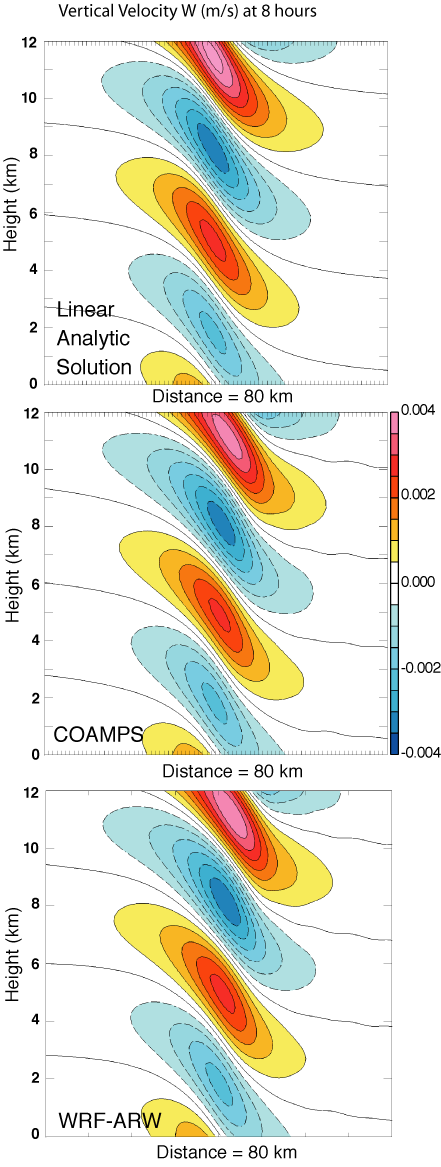
Figure 1.  Vertical velocity obtained for the a) steady-state linear analytic solution, b) COAMPS, and c) WRF-ARW simulations at Ut/a=30 or t=15,000 s.  The vertical velocity contour and color shading interval is 5x10^-4 m s^-1. 

           The vertical flux of horizontal momentum is an additional test of the ability of the model to accurately simulate the properties of vertically propagating linear hydrostatic mountain waves.  The vertical flux of horizontal momentum, defined as

,

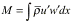where u’ and w’ are deviations from the basic state of the horizontal and vertical velocity, respectively.  The vertical flux of horizontal momentum for linear hydrostatic waves is constant with height (e.g., Eliassen and Palm 1960; Smith 1979)

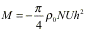,                                                      (3)

where N is the Brunt-Väisälä frequency, which for an isothermal atmosphere can be expressed as,

.

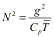The simulated vertical flux of horizontal momentum normalized by the linear flux (3) is shown in Figs. 2a and b for both COAMPS and WRF-ARW, respectively, for the 4, 6, 8, 10 h simulation times corresponding to the Ut/a=29, 43, 58, 72 nondimensional times.  The model-simulated vertical momentum flux reach a range between 0.95 and 1.0, particularly up to a height of one vertical wavelength, Nz/U=6.4 km.  These results are similar in accuracy as a number of other models such as Durran and Klemp (1983) and Xue and Thorpe (1991).  Additional, the evolution of the model simulated surface pressure drag should be compared with the linear drag for a bell shaped mountain, D=prNUh_m²/4, as discussed by Durran and Klemp (1983).

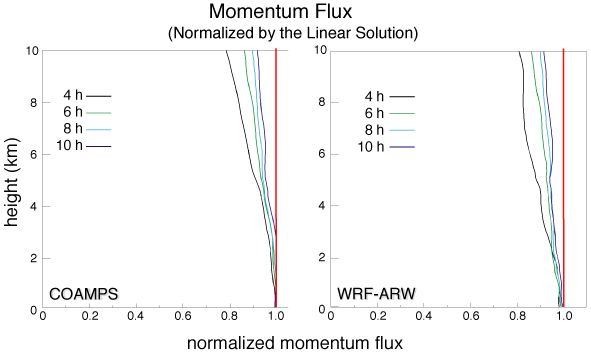
Figure 2.  Vertical profiles of vertical flux ofhorizontal momentum for a) COAMPS and b) WRF.  The vertical fluxes are normalized by the linear values.  The profiles correspond to the 4, 6, 8, 10 h simulation times or nondimensional times, Ut/a=29, 43, 58, 72 and denoted by the black, green, turquoise, and blue colors, respectively.

            This numerical experiment is a robust test for the numerical implementation of model equations including the bottom and top boundary conditions, terrain transformation, and formulation of the vertical velocity and pressure or density predictive equations in nonhydrostatic models.  Since the model terrain height is small in order to minimize the nonlinear effects, the topographic perturbations are small making this experiment sensitive to truncation errors and computational precision issues.  The vertical fluxes are calculated from second order quantities and as a result the momentum flux is particularly sensitive to errors in the velocity fields, while energy flux may suffer from inaccuracies in both the vertical velocity and mass field.  In the example shown in Figs. 1 and 2, the numerically simulated linear hydrostatic mountain waves and associated vertical fluxes of momentum and energy are in very good agreement with the analytic solution.  The mountain waves in this test case are well resolved and should be relatively insensitive to artificial damping and numerical dissipation.

2.  Linear Nonhydrostatic Mountain Waves

Purpose:  This experiment will test the model ability to simulate small-amplitude nonhydrostatic topographic flows.  When the parameter Na/U is approximately unity, both hydrostatic and nonhydrostatic wave components may be present.  The nonhydrostatic waves have a group velocity that is directed with a more downstream component.  The test specifically is designed to assess the accuracy of the nonhydrostatic formulation of the model dynamical equations including the nonhydrostatic solver.  The solutions are also sensitive to the lower and upper boundary conditions and to some degree the lateral boundary conditions because of the downstream dispersion of wave energy.

Analytic Solution:  A linear solution is obtained from the two-dimensional hydrostatic equations of linear mountain wave theory for following Smith (1980).  The linearized equations for the horizontal velocity, vertical velocity, and pressure perturbation are reduced to a single equation for the vertical displacement, h (x, y, z).  A Fourier Transform is used from (x, y) to (k, l) coordinates so that the equation for the transformed vertical displacement 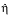 (k, l, z) becomes

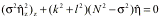,                                         (1)

where s is the intrinsic frequency such that s=Uk+Vl.  The solution to a multi-layer system, which contain constant wind and stability (i=1, 2, 3) is

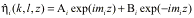,                                          (2)

where the vertical wavenumber is given by m²=(k²+l²)(N_i²-s)/s_i² and A_i and B_i are the amplitude coefficients for the upward and downward propagating waves, respectively.  A radiation condition is applied at the top boundary.  In this application, a single layer with constant stratification of N=0.01 s^-1 and U=10 m s^-1 is considered.  A witch of Agnesi terrain shape with a half-width of 1 km implying Na/U=1.  The analytical solution results for vertical velocity are shown in Fig. 1a. 

Model Setup:  The COAMPS and WRF-ARW models are initialized with uniform stratification of N=0.01 s^-1 and U=10 m s^-1 and a=2 km.  A domain consisting of 360x120 points with Dx=400 m and Dz=250 m.  A Rayleigh damping layer is used in the top 40 layers. 

 

 

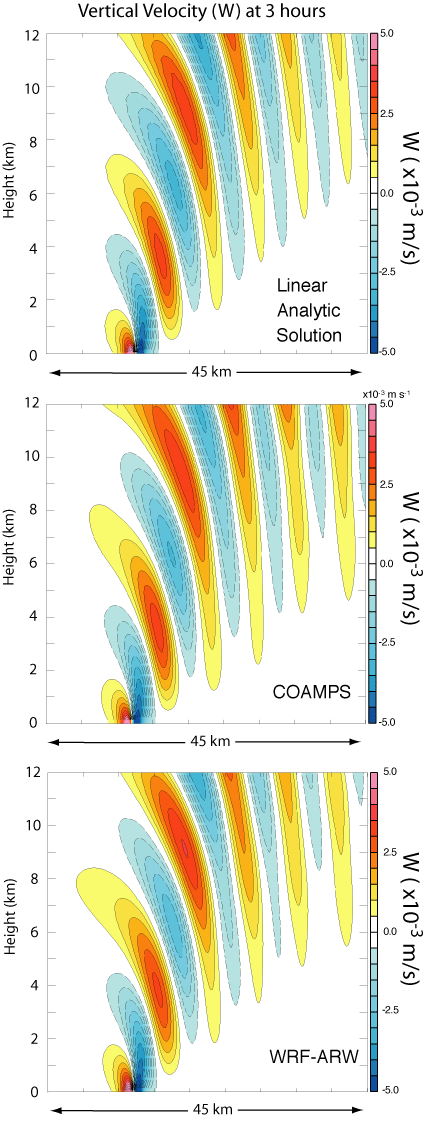
Figure 1.  Analytic solution of vertical velocity (contour interval 6x10^-4 m s^-1) (upper right) for the linear nonhydrostatic test case.  COAMPS (lower left) and WRF-ARW (lower right) simulations of vertical velocity (contour interval 6x10^-4 m s^-1) after Ut/a=45 or 9000 s.