Density Current Test Case

The density current test case is documented in Straka et al, 1993: Numerical Solutions of a Nonlinear Density-Current - A Benchmark Solution and Comparisons. International Journal for Numerical Methods in Fluids, 1-22.  The test case configuration and a multitude of solutions from different models are presented in this paper.

Plotted below is an nearly converged solution from the WRF-ARW model on a 50 meter grid, along with solutions at various other resolutions.  Additionally, there are plots of solutions that have been computed using a constant translation velocity; the level of symmetry between the left- and right-moving currents gives an indication of phase errors, among other things. Model capabilities at reduced resolutions can be examined using this test case, as indicated below.

9 January 2004, W. Skamarock
19 August 2005 - initial condition specification added.  W. Skamarock
7 October 2005 - Updated initial condition specification. W. Skamarock
14 October 2005 - Added discussion, figures.  W. Skamarock

____________________________________________________________________________________________

____________________________________________________________________________________________

 ____________________________________________________________________________________________

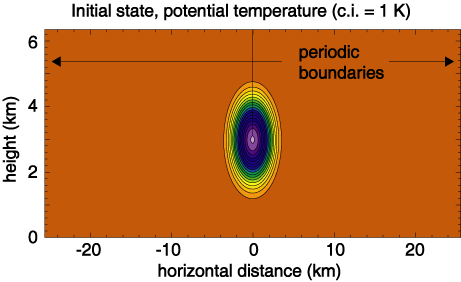
Reference (converged) solution. 

 
____________________________________________________________________________________________

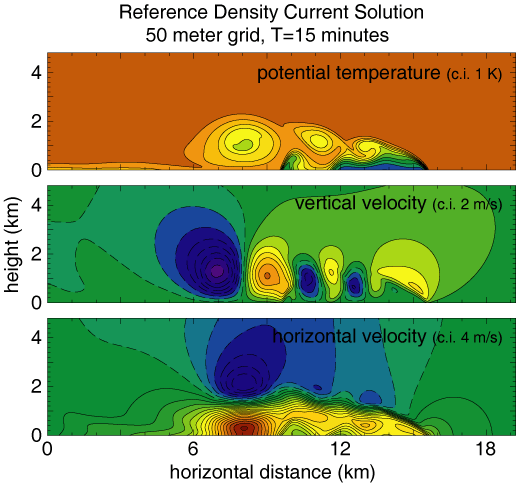
Results using 5th order upwind advection.  The additional filtering in the scheme becomes noticable as the grid spacing is increased.

  ____________________________________________________________________________________________

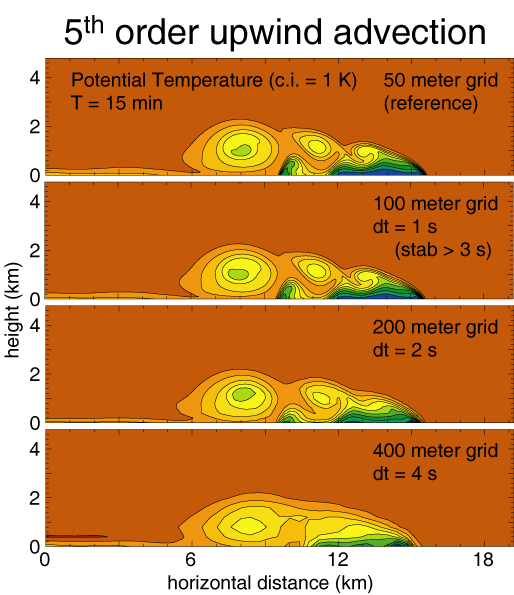
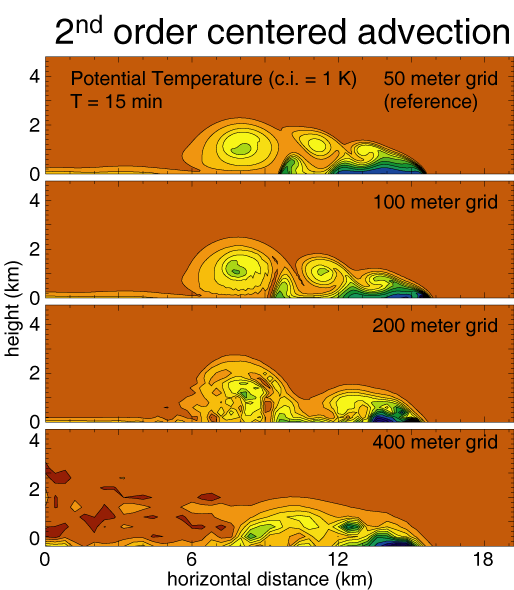
Results using 2nd order centered advection.  The lack of filtering in the scheme becomes noticable with increased grid, and solution errors are noticable even use dx=100 m.

 
  ____________________________________________________________________________________________

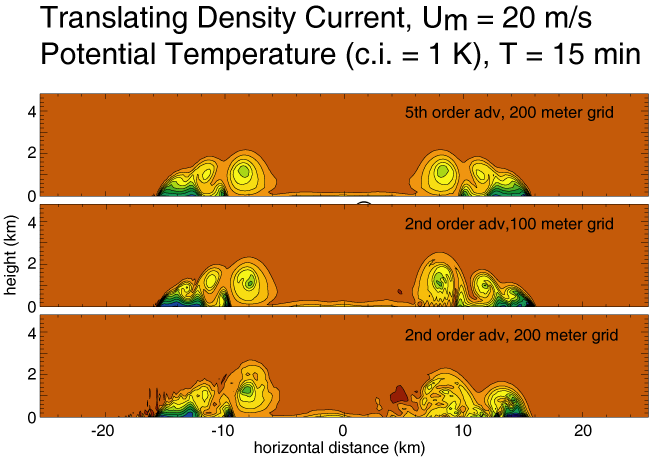
Phase errors as revealed by  translation using a mean wind U_m in a periodic channel.  The solutions should remain symmetric about the center of the channel.

 ____________________________________________________________________________________________

Further Discussion

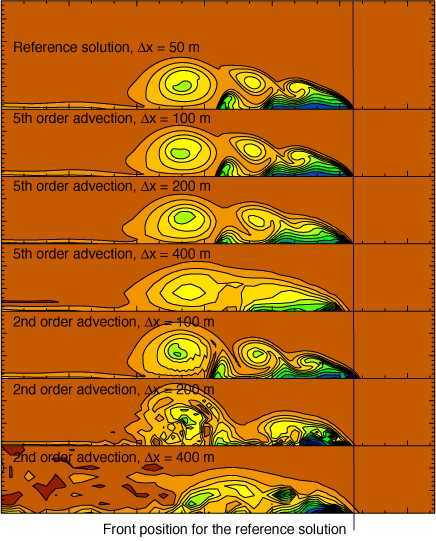
There are a number of integration scheme characteristics that these tests illuminate.  One interesting aspect of the schemes is that the front position at the end time is well predicted even for solutions in which the gravity current is very poorly resolved.  As can be seen in the figure below, the front positions (and by implcation the gravity current  propagation speed) are essentially identical for the dx-50, 100 and 200 m RK3 5th order advection solutions.  The other solutions show small errors in position that result form the large errors apparent in the gravity current structure.

What is also noticable is how the model using  2nd order advection produces a very poor solution at 200 m while the 5th order scheme still produces a reasonable facsimile of the reference (although it does wash out the leading eddy).  The second-order solutions need more computational dissipation at grid-spacings of 100 m or more, but we have not been able to formulate any dissipation for use with the 2nd-order scheme that produces results comparable to the 5th order scheme.  This suggests that the higher order numerics are producing better solutions for this test.

Lower order advection schemes produce noticably poorer solutions in the WRF-ARW model solutions.  Depicted below are the reference and 100 m solutions using5th and 2nd order advection schemes.  The 100 m solution is almost indistinguishable from teh reference solutions when computed using the 5th order advection scheme.  Using the 2nd order scheme, the 100 m solution possesses significant differences in eddy structure compared with the reference solution.  In particular, the eddies are too cold (see arrows below) and the eddies shapes are different (see the first and second eddies rearward of the leading edge).   Truncation errors at the leading edge of the gust front produce anomolously cold air which is ingested into the eddies in the 2nd-order 100 m simulation.  The solutions suggests that the solver would benefit from more numerical dissipation, but experiments show that problems still remain.

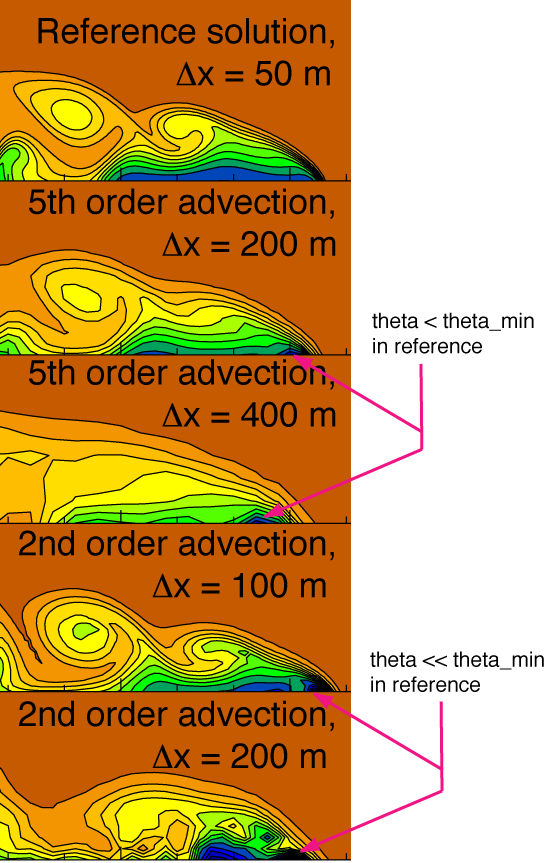
The WRF-ARW advection is not monotonic.  The advection schemes produce undershoots in the potential temperature at the leading edge of the gravity current as illustrated below.  The Lack of numerical damping is particularily pronounced for the 2nd order advection scheme at low resolution.