GPU Acceleration of a Chemistry Kinetics Solver

 

John Michalakes, National Center for Atmospheric Research

John Linford, Virginia Polytechnic Institute and State University

Manish Vachharajani, University of Colorado at Boulder

Adrian Sandu, Virginia Polytechnic Institute and State University

Introduction

This page contains results from work to accelerate an chemistry kinetics solver from WRF-Chem, the atmospheric chemistry and air quality version of the Weather Research and Forecast Model.

WRF-Chem supports a number of chemical kinetics solvers, many of which are automatically generated when WRF-Chem is compiled using the Kinetic Preprocessor (KPP) (Damian, Sandu, et al. 2002). Chemical kinetics is the computationally intensive numerical integration of the time evolution of chemical species and their reactions, which is dominated by the solution of coupled and stiff equations arising from the chemical reactions. The particular solver investigated here is a KPP-generated Rosenbrock gas-phase chemistry solver from RADM2 (see references in article cited above).  Combined with the SORGAM aerosol scheme (see references in WRF-Chem Users Guide), the RADM2SORG  chemistry kinetics option in WRF-Chem involves 61 species in a network of 156 reactions that represent more than 90 percent of the cost of running WRF-Chem over a 60km-resolution domain that is only 40 by 40 cells in the horizontal with 20 vertical layers.  The WRF-Chem time-step for this case is 240 seconds. On this very coarse resolution and very small grid, the meteorological part of the simulation (the WRF weather model itself) is only 160-million floating point operations per time step, only about 1/40th the cost of the full WRF-Chem with both chemistry-kinetics and aerosols.  Only the KPP-generated chemical kinetics solver  is subject of GPU acceleration here; the SORGAM aerosol kernel will be addressed in future work.

Methodology

WRF-Chem was configured, compiled, and run using the small test case described above. The input data to the RADM2 solver was written to files at the call site. The Fortran-90 source files for the RADM2 chemistry kinetics solver that were generated by KPP were isolated into a standalone program that reads in the input files and invokes the solver.  In addition, a number of KPP-generated tables of indices and coefficients used by the solver (described more fully below) were isolated and retained for use in the GPU version of the solver. The timings and output  from the original solver running under the standalone driver served as a baseline for developing the GPU implementation.

The eventual goal is to work with KPP developers and have KPP generate GPU code. However, since it was not yet clear what an optimal GPU implementation looked like, the objective here was to produce a GPU implementation of the RADM2 solver by hand, from the KPP generated source files. Several iterations were necessary.

The first version of the code was a direct Fortran to C to CUDA translation of the KPP generated files.  This was developed and validated against the original code under the CUDA 2.0 emulator running on an Intel Xeon with Linux; however, on attempting to compile under CUDA for the GPU, subsequent to filing a bug report tool stability issues were uncovered and fixed by NVIDIA engineering for the 2.0 versions of the nvcc compiler and ptxas assembler. With the fix, and with raising the default register-per-thread limit (-maxrregcount=85), compilation requires five minutes or less and NVIDIA engineering continues to improve the tool chain. The source of the problem was a number of routines in the solver that were generated in fully-unrolled form by KPP. For example, the KPP solver routine evaluates a sparse Jacobian matrix contains not a single loop but is rather a long succession of assignment statements; likewise code that constructs, LU-decomposes the Jacobian and the equation rates function for the RADM2SORG case, etc. for a total of more than 5000 assignments which appears to overwhelm the register allocation mechanism in the NVCC tool chain (personal communication with NVIDIA). The solution involved both rewriting the chemistry code to “re-roll” these into loops reducing these sections to about 1000 lines. 

 Details of Chemical Solver

The code is a Rosenbrock algorithm for solving stiff systems of ODEs implemented in KPP by Adrian Sandu at Virginia Tech and based on the book Solving ODEs II: Stiff and Differential-Algebraic Problems, by E. Hairer and G. Wanner, Springer –Verlag, 1996.  For chemistry, “stiff” means that the system comprises widely varying reaction rates and that it cannot be solved using explicit numerical methods.  The Rosenbrock technique uses a succession of Newton iterations called stages, each of which is itself solved implicitly.  The implementation takes advantage of sparsity as well as trading exactness for efficiency when reasonable.   An outline of the implementation generated by KPP that was then hand-converted to CUDA is shown below.

The data structures used for the computation at each cell are:

  1. Y(NVAR) – input vector of 59 active species (two less than total 61)
  2. Temporaries Ynew(NVAR) , Yerr(NVAR), and K(NVAR*3)
  3. Fcn(NVAR) – vector of 59 reaction rates
  4. RCONST(NREACT) – array of 159 reaction rates. The variable name is a misnomer; many of these are variable over time and the set of rates is computed separately for each cell.
  5. Jac0(LU_NONZERO), Ghimj(LU_NONZERO) store 659 non-zero entries of Jacobian

Analysis of the computational and memory access characteristics of the program was conducted mostly by hand.  For this case, the chemistry kinetics solution per invocation at each cell of the WRF-Chem grid is computed independently and involves approximately 610-thousand floating point operations and 1-million memory accesses. This is for about 30 iterations of the chemistry solver, and the number of iterations is somewhat dependent on time step. Regardless, although operations is very high (for comparison, the WRF meteorology is about 5-thousand operations per cell-step), computational intensity is low 0.60 operations per 8-byte word and .08 operations per byte.

None of the  small enough to fit in local shared memory without severely constraining number of threads-per-block and thus limiting latency hiding.  The above set of vectors for each cell in the domain were copied to and stored in device memory as a long 1D array. Two layouts of the data in device memory were tried:

            A[ thread-id , vector-len ]

and

            A[ vector-len , thread-id ]

where vector-len is the number of elements on each cell (NVAR, for example). The second layout is slightly more complicated to code, since it involved thread address calculations at the points of the array references; however, this was considerably faster (by a factor of 2) since it allowed neighboring threads to coalesce memory accesses. In other words, the tread index is stride-1 in the second layout.

In addition to the above, “re-rolling” the large loops in the solver introduced a number of additional indirection arrays and arrays of coefficients. 

  1. LU_IROW, LU_ICOL –indirection arrays for 659 non-zero entries of Jacobian
  2. LU_CROW, LU_DIAG – indirection arrays for 60 elements of diagonal
  3. Stoich_Left – 9516 (NSPEC * NREACT) 4-byte float coefficients

These are constant and the same for every cell. Most of these fit in GPU constant memory; the last, STOICH_LEFT is stored in device memory, but accessed as a 2-D texture.

GPU and Cell Chemistry Kinetics Standalone Codes

There are several implementations of the kernel that may be downloaded from this site.

Codes:

The original "vanilla" Fortran version with an option to run multi-core using OpenMP threading is available here:

            http://www.mmm.ucar.edu/wrf/WG2/GPU/Chem_benchmark/chem_bench_omp.tar.gz

The most recent GPU version (updated July 2010; fixes gfortran endian problem and will run on Fermi) is here:

            http://www.mmm.ucar.edu/wrf/WG2/GPU/Chem_benchmark/radm2_cuda_masked_20100723.tar.gz

Linford and Sandu’s Cell implementation of the kernel may be downloaded from:

 http://www.mmm.ucar.edu/wrf/WG2/GPU/Chem_benchmark/cell.tar.gz (0.42 MB).

Input datasets:

The dataset for the small workload is here:

            http://www.mmm.ucar.edu/wrf/WG2/GPU/Chem_benchmark/radm2sorg_in_001.gz

The large workload is here:

            http://www.mmm.ucar.edu/wrf/WG2/GPU/Chem_benchmark/radm2sorg_in_010.gz

 

Instructions:

These instructions are out of date.  Need to be updated.  To compile, edit the makefile and then type make.  To run the benchmark, cd to the run directory and type ./runit .  There is a SAMPLE_SESSION file in the top-level directory to compare against. If both the original and GPU versions of the code run successfully, the script computes RMS error (5.53492e-12) for one of the output chemical species (Ozone). Your result should be close to this (same order of magnitude or less). For newer versions of code see README in distribution.

Results (Updated 9/7/2009)

The GPU version of the chemistry kernel is invoked for a chunk of cells in the large array of cell states. But chunk-size and block-size (the number of threads per block) is variable and specified when the standalone chemistry code is invoked.  Parameter sweeps over chunk-size and block-size revealed that a single chunk of all 28,889 cells in the domain and a block-size of 192 threads per block was most efficient.  Block sizes larger than 192 cells fail to run, presumably because each thread uses 85 registers and larger blocks exceed 16K available.

The test system was a GPU cluster at NCSA, ac.ncsa.uiuc.edu:

The best time achieved on a C1060 Tesla GPU for this double precision workload was 6.9 seconds, including host-GPU data transfer time.  Running single precision, the best time was 3.3 seconds. 

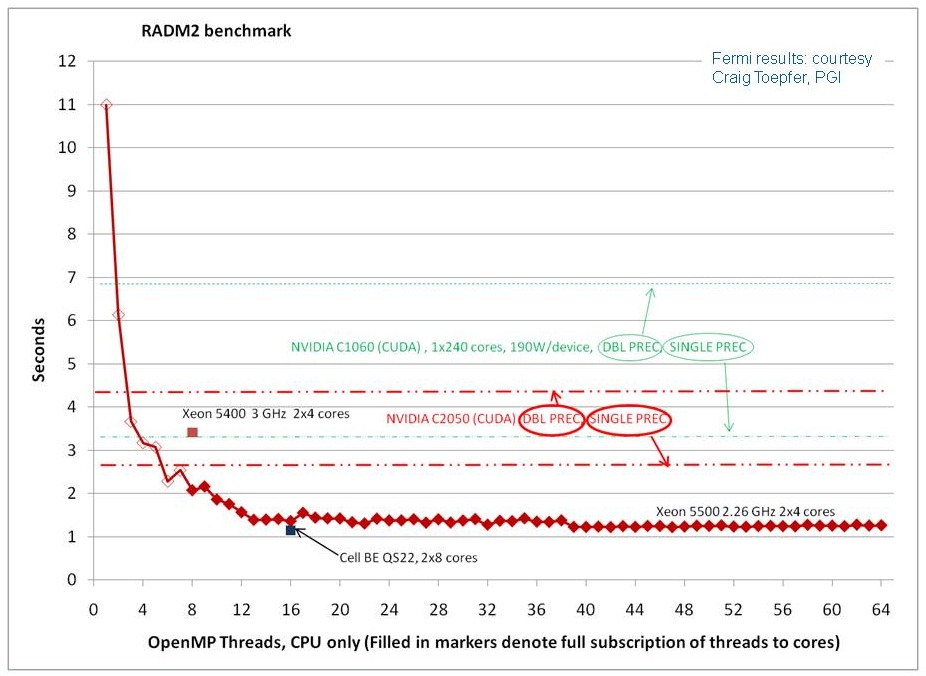
The plot below shows results running the original “vanilla” Fortran version of the benchmark, modified to run multi-threaded using OpenMP, on new Intel Nehalem processors.  (The modified code is here). The blue line shows seconds to compute the workload on a Mac Pro (joshua.mmm.ucar.edu) with two quad-core 2.26 GHz Nehalem processors.  The x-axis is increasing number of OpenMP threads up to 64 threads (always only 8 physical cores).  The notch at 16-threads is for 2-threads per core.  The code was compiled using Intel Fortran 11.0 with -fast optimization.  For comparison, earlier results for 8-threads on a 3 GHz dual-quad core Xeon 5400 (John Linford at Virginia Tech) are plotted. This was with a C version of the OpenMP code. Also, for comparison, the best time achieved for the CUDA implementation of the benchmark on a Tesla C1060 GPU is indicated with the dashed green lines, double and single floating point precision as indicated. (update July 2010) The dashed red lines show single and double precision on the Tesla C2050 (Fermi). Our assumption is that single precision performance improves relative to C1060 because of the larger number of cores and the larger number of registers. The gap between double and single precision performance is narrower because of the increased number of special function units (SFU) in the Fermi.

Preprint

            J. Linford, J. Michalakes, A. Sandu, and M. Vachharajani, Multi-core acceleration of chemical kinetics for simulation and prediction, in proceedings of the 2009 ACM/IEEE conference on supercomputing (SC'09), ACM, 2009.

Acknowledgements

Placeholder for now. Make sure these are mentioned:

 

 

Last updated, July 23, 2010   michalak@ucar.edu