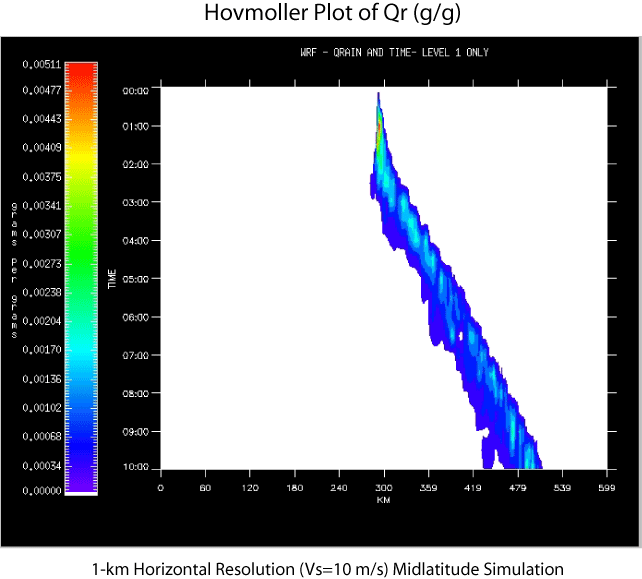
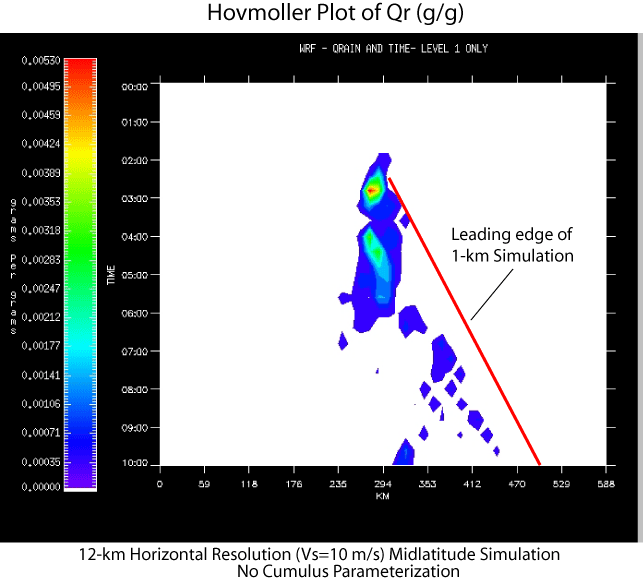
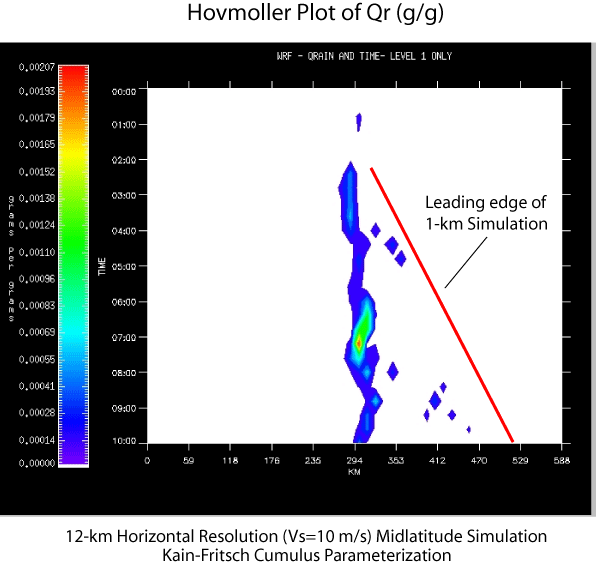
A series of tests with mass coordinate version of the WRF model have been designed to examine the sensitivityof deep convection simulated using different physical parameterizations for different model domain configurations (e.g., 2D, 3D periodic), grid resolutions and different meteorological thermodynamic and flow regimes.

Figures 1-3 portray an example of such a test for a 2D simulation of deep convection in a warm-season midlatitude environment of large convective available potential energy (CAPE = 2800 J/kg) and weak-to-moderate vertical wind shear (delta U = 10 m/s through the lowest 3 km). A density-weighted mean wind of approximately zero averaged through the depth of the troposphere was specified in the initial condition of these simulations which utilized the Lin et al. microphysics parameterization (mp_physics = 2) and no PBL parameterization (bl_pbl_physics = 0). In these particular experiments deep convection was initiated by a semi-infinite surface based cold pool placed in the left (upshear) side of the domain spanning x = 0-300 km at t = 0. The Hovmoller diagram of surface rain water mixing ratio for a control simulation at 1-km horizontal grid spacing (Fig. 1), which explicitly resolves deep convection, shows an eastward propagation of the leading of the precipitation system (u ~ 7 m/s) between t = 2 and 10 h. In this simulation the precipitation cells that are triggered on the downshear edge of the cold pool are quasi-stationary in the environment of near-zero mean flow, and move rearward relative to the leading edge of the system (Fig. 1). Some aspects of this simulation are captured in a simulation that uses a horizontal grid spacing of 12 km (Fig. 2), however, convection is triggered somewhat later and eastward propagation is not evident until ~ 6 h. A simulation with the same coarse grid spacing of 12 km and employed the Kain-Fritsch cumulus parameterization (cu_physics = 1) in Fig. 3 evinces some development of weak cells ahead of quasi-stationary precipitation system. From this example it is clear that while a "coarse" resolution simulation that utilizes convective parameterization is able to predict the occurrence of a mesoscale precipitation system it does not adaquately predict the evolution of its structure and propagation characteristics.